From Yoneda Embedding …
Yoneda Embedding is said to be a generalization of cayley theorem, which I don’t know if is true since I never learned group theory. And an important theorem about Yoneda Embedding can also be generalized to Yoneda Lemma.
Functor $Y: {\cal C}^{op} \rightarrow {\textbf{Func}({\cal C}, \textbf{Set})}$ is Yoneda Embedding, where ${\textbf{Func}({\cal C}, \textbf{Set})}$ is the category where the objects are functors and arrows are natural transformations. Below picture is from https://bartoszmilewski.com/2015/10/28/yoneda-embedding/.
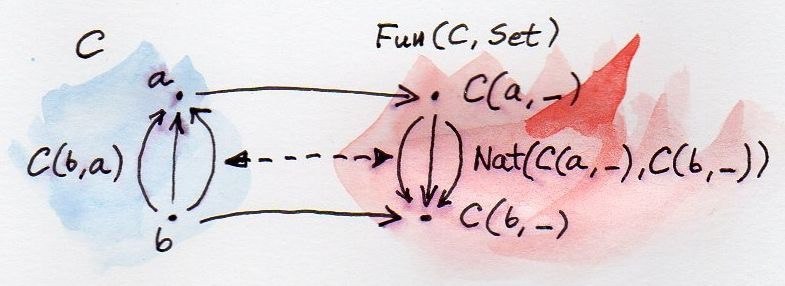
Specifically, $Y(C) := Hom_{\cal C}(C, \cdot)$. Let’s see what definition can make it into a functor. For arbitrary arrow $f:A \rightarrow B \in {\cal C}$, we have $f’:B \rightarrow A \in {\cal C}^{op}$. Then $Y(f’) : Hom(B, \cdot) \rightarrow Hom(A, \cdot) : {\cal C} \rightarrow \textbf{Set}$. Thus $Y(f’)$ has to be a family of arrows s.t. the following commutative diagram holds
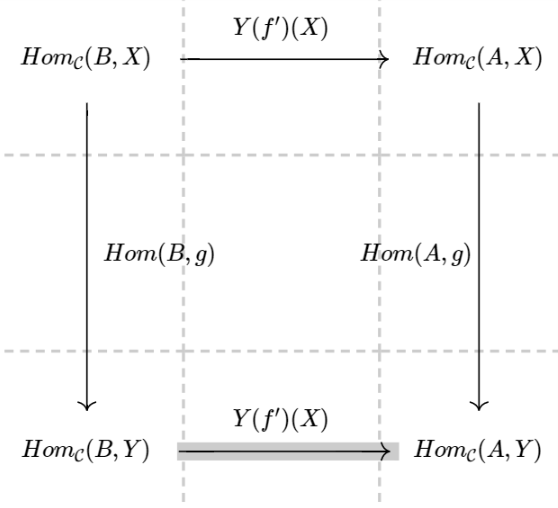
It is easy to see that $Y(f’)(X) := { g \mapsto g \circ f}$ can make this diagram commute and the truth is Yoneda Embedding is defined like it.
Now we can come to the important theorem.
$Y$ is full and faithful. In other words, for arbitrary $C,D \in {\cal C}$,
Those $Hom_{\cal C}(C, \cdot) \rightarrow Hom_{\cal C}(D, \cdot)$ 1-to-1 correspond those $C \rightarrow D$.
Due to 3.3.11 of Barr and Wells, thus $Hom_{\cal C}(C, \cdot) \cong Hom_{\cal C}(D, \cdot)$ implies $C \cong D$.
Proof of full and faithful.
<summary>To Show Full:</summary>
<p>
Take arbitrary $\eta :Hom_{\cal C}(C,\cdot) \rightarrow Hom_{\cal C}(D, \cdot)$, we claim that
$$Y(\eta_C(id_C)) =^? \eta$$
To show which, in turn we need take arbitrary $X \in {\cal C}$ and (since $Hom{\cal C}(C,X)$ thank-god is a set) an arbitrary arrow $f\in Hom_(C,X)$,
$$Y(\eta_C(id_C))_X(f) =^? \eta_X(f)$$
To show which, by simplification, we need
$$f \circ (\eta_C(id_C)) =^? \eta_X(f)$$ and we have the following commute diagram since we have $\eta$ as natural transformation:
<img src="/assets/img/2019-08-27-21-43-59.png">
</p>
<summary>To Show Faithful:</summary>
<p>
Since for arbitrary $f: D \rightarrow C$, $Y(f)_C(id_C) =id_C \circ f = f$,
that means $Y(f_1) = Y(f_2)$ implies $f_1 = f_2$.
</p>
$\blacksquare$
This is the theorem which is a generalization of cayley theorem.
… to Yoneda Lemma
It is not easy to see that the theorem can be generalized further.
Let $F : {\cal C} \rightarrow \textbf{Set}$ be a set-valued functor,
Those $Hom_{\cal C}(C, \cdot) \rightarrow F$ 1-to-1 correspond those in $F(C)$.
By take $F = Hom_{\cal C}(D, \cdot)$, we can get the above theorem. But this correpondence is no longer relevent to any functor, i.e. it is not a correspondence between categories, but just a bijection between sets.
But here we need to construct a mapping just like Yoneda Embedding which maps elements in $F(C)$ to natural transformations, but we have no clue what it looks like. Since taking $F = Hom_{\cal C}(D, \cdot)$ can lead to that theorem, we are supposed to generalize something out of the Yoneda Embedding. Recall we have Yoneda Embedding (the part of mapping arrows):
For $f : D \rightarrow C [= Hom(D, \cdot)(C)]$,
For $X \in {\cal C}$,
For $h \in Hom(C,X)$,
$Y(f)_X(h) [\in Hom(D,X)] := Hom(f,\cdot)(X)(h) = h \circ f = Hom(D,h)(f)$
We abstract away $Hom(D,\cdot)$, (do you see something like dependent type Programming? The rewrite we do have to make this huge term well typed, and that is the reason why we rewrite $h \circ f = Hom(D,h)(f)at the end$ before we ‘patterned’ away $Hom(D,\cdot)$) and get
For $F : {\cal C} \rightarrow$ Set,
For $f : F(C)$,
For $X \in {\cal C}$,
For $h \in Hom(C,X)$,
$Y_2(f)_X(h) [\in F(X)] := F(h)(f)$
and now the mapping $f \mapsto Y_2(f)$ is the mapping from $F(C)$ to those natural transformations.
Surprisingly, either for the proof of injective or surjective, we just need again abstract away all the $Hom(D,\cdot)$ (or $D \rightarrow \cdot$) into $F$ and we are done. There is even no non-trivial rewrite.
Representable Functor / Universal Elements
A set-valued functor, $F : {\cal C} \rightarrow Set$, is representable if $F$ is naturally isomorphic to $Hom_{\cal C}(C, \cdot)$ for some object $C$ in ${\cal C}$. In that case, we will also say $C$ represents $F$.
*Note that, if $F$ contravariant, then the hom functor would be $Hom_{\cal C}(\cdot, C)$. *
For the above $Y_2$, if $Y_2(\cdot)(f)$ turns out to be a natural isomorphism, then we call $f$ a universal element. And this natural transformation is induced by $f$.
It is trivial to see that, due to Yoneda Lemma, if there is a natural isomorphism, then it must be induced. When the natural isomorphism is $\eta : Hom(C,\cdot) \rightarrow F$, the corresponding universal element is $\eta_C(id_C)$ because $Y_2(\eta_C(id_C)) = \eta$ which is shown in the proof of surjective in Yoneda Lemma and proof of full in Yoneda Embedding.