Final lecture note of MAT347 Winter 2021.

Galois Theory

• If $K/F$ is a field extension
  • $\langle Aut(K), \circ \rangle$ is the group of automorphism (field homomorphism)

    Definition: $Aut(K/F)$

• $Aut(K/F)$ is a subgroup of those automorphism that fix $F$
  • i.e. $\sigma x = x \quad \forall x \in F$
• For any $K, F$, $id \in Aut(K/F)$ ***
• $\Complex / R$ where $z \mapsto \overline{z}$ fixed $R$
  • so conjugation is an element of $Aut(\Complex/R)$ ***
• Prime Field in $K$ is generated by $1$
  • if $\sigma \in Aut(K), \sigma 1 = 1$
  • thus $\sigma$ fixed the prime field
• Thus $Aut(K) = Aut(K/K_{prime})$ ***

  Prop:

• Suppose $K/F$ and $a \in K$ is algebraic over $F$
  • if $\sigma \in Aut(K/F)$
    • then $\sigma a$ is a root of $\min_{a,F}(x)$
      • which is $g \in F[x]$ s.t. $g(a) = 0$
• An example is $x^2 + 1 = 0$ has conjugated roots
• the reason is that you can apply $\sigma$ to it and by homomorphism you can see that ***
• If we live in a ground field $F$,
  • $f\in F[x]$ if $f(a) = 0$ then $f(\sigma a) = 0$
    • you cannot easily distinguish by using language like $f$
      • using term from lower field

        Prop:

• Suppose $H \subseteq Aut(K)$
  • Define $F_H = {x \in K : \sigma x = x \quad \forall \sigma \in H}$
    • then $F_H$ is a subfield of $K$
      • $F_H$ is the fixed field of $H$ ***
• If $F$ is a subfield of $K$ is a subfield
  • then we can associate $Aut(K/F)$ to $F$

    Galois Theory: Association between Subgroup of $Aut(K)$ and subfields of $K$

• Easy : reverses inclusions: smaller fields corresponds to bigger subgroup

  Prop:

• Suppose $E$ is the splitting field of $f(x) \in F[x]$ (contains all the roots of $f$)
  • then $|Aut(E/F)| \le [E : F]$
  • $|Aut(E/F)| = [E:F] \iff f(x)$ is separable (can become linear factors, splits completely $E$) (???)
    • separable : its roots are distinct in an algebraic closure of K, that is, the number of distinct roots is equal to the degree of the polynomial
    • only one issue in character = p
• proof: $F(a) \mapsto F(\sigma a)$ will be extends to $E \mapsto E$

Definition: Galois Extension

• A finite extension $K/F$ is galois (A Galois Extension) iff $Aut(K/F) = [K:F]$
• In that case $Aut(K/F)$ is called Galois Group of $K/F$
• Example:
  • $\Complex/R$ where $\sigma : z \mapsto \overline{z}$
    • $Aut(\Complex/R) = Gal(\Complex/R) = {e, \sigma}$
    • $[\Complex : R] = 2 = |Aut(\Complex / R)|$
  • $Q[\sqrt{d}]/Q$ is of degree 2
    • then $Aut(Q(\sqrt{d}/Q)) = {e, x+\sqrt{d} \mapsto x - y \sqrt{d}}$ ***
• Example: Galois Theory
• 
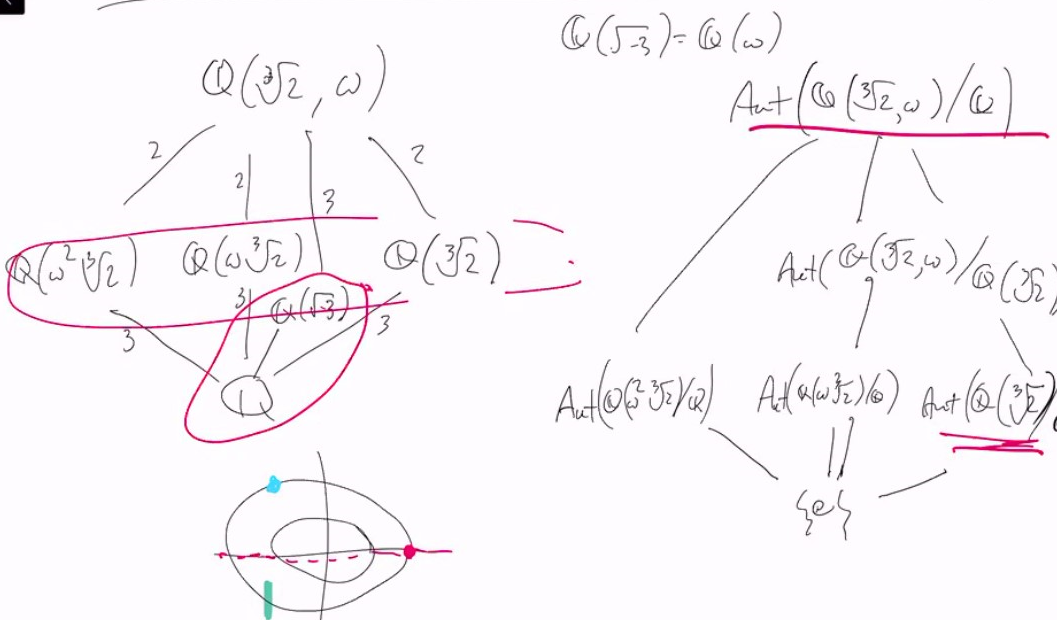
  • there are some Galois Extension inside the picture
  • normal extension ~normal subgroup
    • quotient on the normal subgroup ~ galois group
    • section 14 ***
• $f(x) \in F[x]$
  • if take $a^{\frac{1}{m}}$, we will have an extension $a^{\frac{1}{m}}$
    • cyclic extension on galois group
    • 
    • requiring galois group is a solvable group
    • $S_2,S_3, S_4$ are solvable, but $S_5$ is not
      • but “most” of 5-th power has $S_5$ as Galois Group
• Legend says Galois finish all these in one night